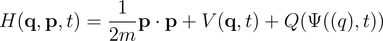History
Prof.Yang did the research about the connection between quantum mechanics and classical mechanics by himself since 1998. He tries to answer some questions which cannot be explained well by quantum mechanics, for example, tunnel effect, multi-path, double slits interference, etc. Furthermore, he also tries to answer what is the essential of the Schrodinger equation, the formation of matter wave and the origin of the operator, which have no explanation providing by quantum mechanics. Prof. Yang develops this theory following the deterministic concept to approach to the quantum world. With having the help of Chinese culture, which claim that there are two parts of our world, one is "Yang", and the other is "Yin", corresponds to the "real" world and "imaginary" world, respectively. Prof. Yang attempts to expand the dimension of Newtonian mechanics to the complex domain. A spectacular result comes out that quantum mechanics becomes compatible with Newtonian mechanics under the framework of complex space. k
With this complex extension, he shows that quantum mechanics becomes a part of analytical mechanics and hence can be treated integrally with classical mechanics. Complex canonical variables are governed by Hamilton equations of motion, which can be derived naturally from Schrodinger equation. Using complex canonical variables, a formal proof of the quantization axiom, which is the kernel in constructing quantum-mechanical systems, becomes a one-line corollary of Hamilton mechanics. The derivation of quantum operators from Hamilton mechanics is coordinate independent and thus allows us to derive quantum operators directly under any coordinate system without transforming back to Cartesian coordinates. Besides deriving quantum operators, we also show that the various prominent quantum effects, such as quantization, wave-particle duality, tunneling, atomic shell structure, Aharonov-Bohm effect, and spin, all have the root in Hamilton mechanics and can be described entirely by Hamilton equations of motion.
Bohr's view about the wave function is that due to its expression in terms of imaginary numbers, wave function is not susceptible to pictorial interpretation; and even the derived real functions like densities and currents are only to be regarded as expressing the probabilities for the occurrence of individual events. Accordingly, orthodox (Copenhagen) quantum mechanics contain no statement regarding the objective constitution of matter corresponding to the conception of particles and fields employed in classical physics. There are no “electrons” or “atoms” in the sense of distinct localized entities beyond the act of observation; without measurement, there is no objective existence. Orthodox quantum mechanics asserts that electrons and “atoms” only exist in the instant of measurement; nothing can be said between measurements.
Since Max Born's statistical interpretation of wave functions, there has been the long-standing problem of “interpretation of equations”. However, the emphasis should not merely be on “interpretation”: The right problem to set is
“What is the Schrodinger equation?”
In quantum mechanics one can only compute the expectation of physical quantities. Because orthodox quantum mechanics does not possess equations of dynamics, when one learns quantum mechanics, one has to develop one's own personal sense or picture to interpret the theory. It is safe to say that the lack of the equation of dynamics has been the primary source of controversies about the interpretations of quantum mechanics, although it has the equation of propagation of probability, i.e., the equation. Therefore, a plausible answer to the problem of “what is the Schrodinger equation?” relies on the help of establishing equations of dynamics compatible with equation.
Complex Mechanics (Quantum Hamilton Mechanics)
The readers will
find in this theory that the equations of dynamics compatible with are
just
the classical Hamilton equations extended to complex domain. By employing
complex-extended Hamilton equations, there will be no ambiguity at all in under-
standing the motion of quantum particles, in other words, we no longer need the so-
called “interpretation”. Everything becomes transparent and
every quantum mechanical
problems can be solved by the well-established
methods in analytical mechanics. The
following figure highlights the features of complex mechanics.
The Hamiltonian for quantum systems is complex-valued